New Version of ToonTalk Numbers
This page describes numbers, including many improvements were made to numbers beginning with beta 34 (or release version 2.50 or greater). Click here to read about the old version.
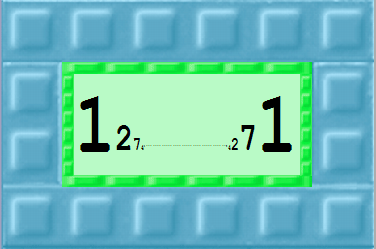
If you drop a number, for example, 2, on another number, say, 7, they will be added by Bammer turning the 7 into a 9 and destroying the 2. If you type the key for an operation before dropping the 2 then the following will happen:
x or * multiply (7 x2 becomes 14)
/ divide (7 /2 becomes 3) SHOW ME
% remainder (7 %2 becomes 1) SHOW ME
^ to raise to a power (7 ^2 becomes 49) SHOW ME
= set to number on top (7 =2 becomes 2 as does any number with =2 dropped on it) SHOW ME
- makes the number negative (7 plus -2 becomes 5)
You can change a number when holding or pointing to it by typing. You can also drop a number on a notebook to go to that page number. If you drop a number on a text pad you'll change the first or last letter depending on which side of the pad you dropped it. If, for example, you dropped 2 on the right side of the text pad containing "ABC", it'll be turned into "ABE".
Blank numbers.
A blank number pad can be any number. They are handy inside of a robot's thought bubble. This way a robot will only accept a box with a number where the blank number is. This corresponds to a "type test" in conventional programming languages.
They can also be used for something called "type conversion". You can change a text pad that is showing a number into a number by dropping it on a blank number pad. SHOW ME Or you can take a box and drop it on a blank number pad and the pad will end up showing how many holes the box has. You can even drop a team of robots on a blank number pad to find out how many robots there are. Dropping a notebook on an erased number pad turns the pad into the number of pages in the notebook. You need to use Dusty to remove the number from a pad to make it blank. SHOW ME
The following operations on numbers as strings of bits are supported as well but only advanced users need to worry about them.
~ complements or negates all the bits (~2 becomes -3 since it is two's complement)
& bitwise and of numbers (7 &2 becomes 2 or in binary 111 AND 010 becomes 010)
| bitwise or of numbers (7 |2 becomes 7 or in binary 111 OR 010 becomes 111)
Arbitrarily large integers.
This means that numbers behave as they should and not as they do in nearly every other programming language. In the earlier version of ToonTalk all numbers needed to be between 2147483647 and -2147483648. Now the only limit is the amount of memory need to store a number. Numbers with 100,000 digits work just fine however some operations may take a noticeable amount of time. Multiplying two 100,000 digit long numbers may freeze ToonTalk for a few seconds.
Prior to 3.107 or beta 45, ToonTalk would crash or exit when displaying a number with more than about 750,000 digits. The limit was raised to 7,500,000 in version 3.107. Numbers larger than this can still be used in computations but they display an explanation that ToonTalk can't compute the digits. Even larger numbers can be displayed in a base that is a power of two (e.g. hexadecimal or base 32).
Beginning with 3.125 or beta 46, if the number pad is in a box or notebook or its size has been changed by Pumpy and there isn't enough room to display all the digits then the first and last digits are displayed at full size and the digits in between are displayed as shrinking to dots and then growing again. (This feature can be turned off using the toontalk.ini OKToDisplayNumbersShrinkingAndGrowing switch.) Here is the 37th Mersenne prime which has 909,526 digits: SHOW ME (this will pause for a few seconds while computing)
Exact rational numbers.
In the older version division always returned the quotient and threw away the remainder (though using % you can get the remainder). So dropping "/3" on "4" used to result in "1" while now it results in "4/3". This is not approximated internally but is stored exactly with a numerator and denominator that can be as long as needed. For example, dropping "*6" on to "4/3" will result in exactly "8".
Beginning with Beta 39 (or version 2.99g) there is
a new way of displaying numbers that are fractions that cannot be shown as exact
decimals. The idea is to have the digits shrink as they approach the right side
of the number pad. Here is 1/7:
SHOW ME
A number like "3/2" can be displayed as either 
or 
or 
. At the beginning of the notebook on
page 12 of your main notebook you'll find four styles of displaying rational numbers. They
are
Fraction. A numerator over a denominator where they have no common divisors and hence are as small as possible.
Integer followed by a proper fraction. The closest integer to the number (from zero) followed by a proper fraction. The sum of the integer and fraction is exactly the number.
Exact decimal or fraction if no exact decimal exists. Same as number 1 except it will display as a decimal number if it can do so exactly.
Exact decimal or an integer followed by a proper fraction if no exact decimal exists. Same as number 2 except it will display as a decimal number if it can do so exactly.
You can use choose among the four sample numbers in the notebook on page 12 to control which format is used. Also if you erase one of these numbers and drop a number with a different format on top, it'll be converted to the format of the erased number.
Fractions are displayed as follows (unless this feature is turned off by setting OKToDisplayNumbersShrinkingAndGrowing to 0 or the internal version number is less than3.125):
and
.
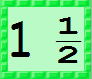Sensors and rational numbers.
Most numeric sensors truncate whatever value they are given to an integer. The only exceptions are a picture's sensors for its x and y position, width and height, and x and y speed. These can now have fractional values. By default only the speed sensors display the exact value - the other sensors display their integer value. You can override this by adding "-integer_positions 0" to the command line.
Editing and typing numbers.
Beginning with version 3.78 or beta 43 you can now type numbers even if the intermediate states are syntactically incorrect. It is only when dropped or when deselected does the newly typed number gets updated. If the result is syntactically incorrect the number reverts to its previous value. You can also use arrow keys to edit numbers (except the shrinking digits since they are infinitely long).
Changes to operations.
It has always worked in ToonTalk to pick up a number, say 5,
and type '\' and it becomes '\5' which is the operation of dividing by 5. You can drop it
any number and it'll divide that number by 5. But "\5" isn't really a number, it
is an operation on numbers. To help make this distinction clear the color of operations is
somewhat different from numbers. So "\5" looks like 
.
What should happen if "2" is dropped on
"\5"? The result in the old ToonTalk was "\7" as if you operating on
the number part of the operation. Now the operations are concatenated so the result is 
. This is an
operation that will divide by 5 and then add 2 to the result.
SHOW ME
New Operations.
Exponentiation. There is one new operation that you can type. It raises a number to a power. You can type "^" to any number to turn it into the power operation. For example dropping "^3" on to "5" will result in "5x5x5" or "125". If the number is negative then the reciprocal of the result results. "^-3" on 5 results in "1/125" or ".008". The exponent can be fractional as well to compute roots like square root. Dropping "^1/2" on 9 results in "3". Dropping "^3/2" on "9/4" results in "27/8" since the square root is 3/2 and cubing that is 27/8.
Whenever ever possible ToonTalk will try to compute an exact result when taking a root of a number. When there is no rational root then an approximation is used. It is displayed in gray to indicate that it is an inexact number. (See below for more about inexact numbers.) For example, dropping "^1/2" on "2" will result in an inexact approximation of the square root of 2.
Calculating an even root of a negative number should result in an imaginary number. It currently fails and Marty explains that some arithmetic couldn't be done.
In the notebook on page 12 you'll find the following new operations:
Integer Part. Throws away the fractional part. Does nothing if the number is already an integer.
Fraction Part. Throws away the integer part. Becomes zero if the number is an integer and therefore has no fractional part.
Numerator. Becomes the numerator. Does nothing if the number is already an integer.
Denominator. Becomes the denominator. Becomes one if the number is an integer.
And the following operations return inexact values even when there is a correct exact rational value (e.g. Log 10 of 10 is 1.000000 rather than exactly 1):
Sine. Becomes the sine of the number it is dropped on. It treats the number as an angle in degrees.
Cosine. Becomes the cosine of the number it is dropped on. It treats the number as an angle in degrees.
Tangent. Becomes the tangent of the number it is dropped on. It treats the number as an angle in degrees.
Arc Sine. Becomes the inverse sine in degrees of the number it is dropped on.
Arc Cosine. Becomes the inverse cosine in degrees of the number it is dropped on.
Arc Tangent. Becomes the inverse tangent in degrees of the number it is dropped on.
Natural Log. Becomes the natural log of the number it is dropped on.
Log Base 10. Becomes the log base 10 of the number it is dropped on.
All of the binary operations (+, -, *, /, %, ^, |, and &) can be rubbed out (using the 'Backspace' key) so that the operation remains without any numbers. This can be given its first number value by dropping it on a number or by dropping a number on it. It then becomes an ordinary operation that can be dropped on another number.
Inexact numbers.
The trigonometric operations above and the log operations produce inexact results. Sometimes the exponential operation also produce inexact results but only if the result is irrational. All other operations produce exact results if given exact inputs. ToonTalk represents these inexact results (when they are between 10308 and -10328) internally as 64-bit IEEE floating point numbers. Any operation where at least one of the numbers involved is inexact has an inexact result. The only exception is the "=" operation that makes the number underneath equal to the one being dropped. In this case the exactness depends only upon the number with the "=" operation.
Tiny round-off errors are common and may accumulate. Inexact numbers work like ordinary numbers but are displayed in gray to remind you that they are inexact.
If you drop an inexact number on an erased exact number it'll be converted to the closest equivalent exact rational number.
Bases.
You can view or type numbers in any base between 2 and 36. SHOW ME
Speed and memory issues.
Very large integers and exact fractions can on occasion take a very long time to compute, display, save, or load.
home | search | purchase | manual | news | info | games | faq | support | downloads | endorsements | press | contact us